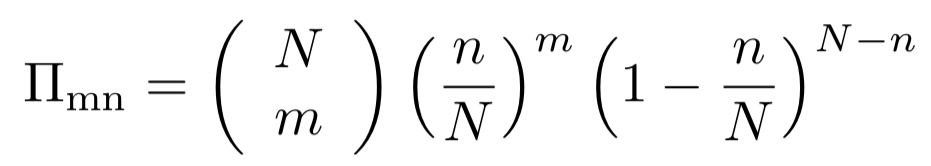Mutation

Effect of mutations on diversity

Apart from the genetic drift we discuss in the last chapter, mutations are often involved with evolutions. Mutations can result from:

errors during DNA replication
damage to DNA (such as caused by exposure to radiation or carcinogens)
insertion or deletion of segments of DNA due to mobile genetic elements

On one hand, mutations provide materials for natural selections. Generally mutations may or may not produce changes in the phenotype of an organism. On the other hand even if without natural selections, the process of mutation still effect the frequency of alleles. We will see the simulation combining the effect of drift and mutation in next chapter. Later we introduce a mathematical description for these two processes and discuss the balance status.

Figure source: https://pokemontownship.deviantart.com/journal/Mutation-Guide-663165036

Simulate genetic drift and mutation

We perform a simulation of genetic drift and mutation together. For the drift side, all the assumptions are same with the previous chapter. Therefore, the difference of the result here from the one in the previous chapter is the effect from mutations. The probability of the two alleles to each other is same (1%). To study the result of the population size, the simulations use size of 20, 200 and 2000. Here, only a gene with two alleles (red and blue) is considered. The plots shown below are the frequency of red allele as a function of generation.

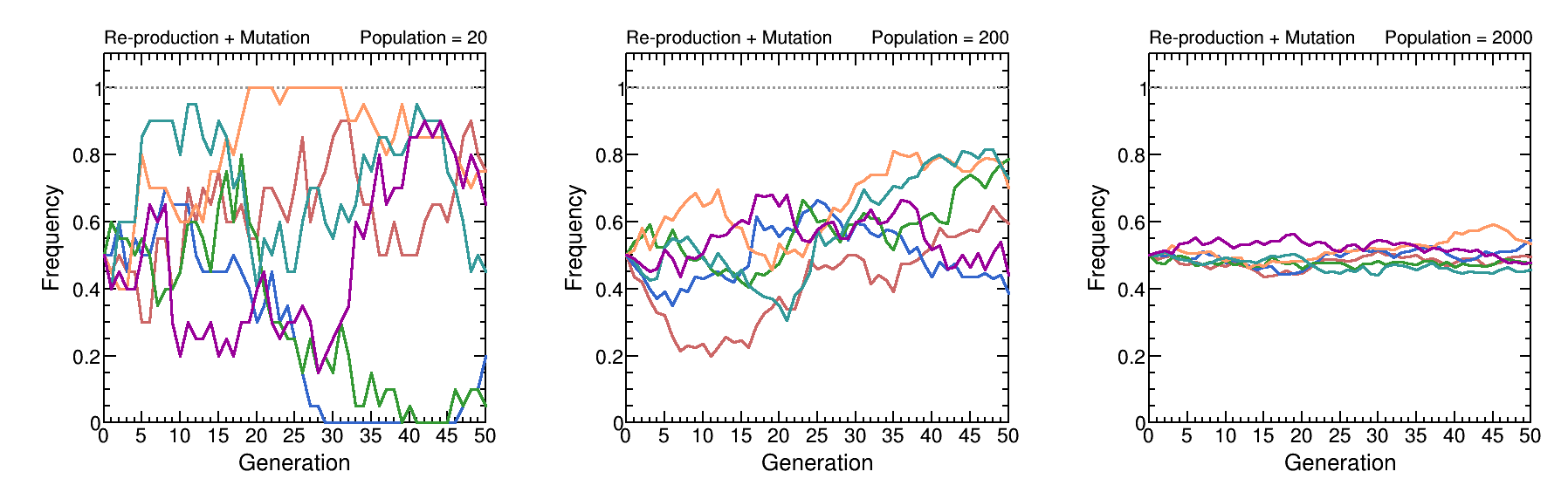
We can see there is no fixation or loss for a specific allele, because even if an allele is lost, it is still possible to appear again due to mutation. Therefore, genetic drift reduces the genetic diversity, while mutation increases the genetic diversity at the same time. They effect the dynamics of a population together. In next chapter, we will build a simple mathematical model to describe these two processes and discuss their roles under different configurations.

Mathematical description

Probability density and the forward Kolmogorov equation

Let's consider a system with population size of N with a gene with two alleles (A₁ and A₂). To describe the frequency of one alleles, if there are n individuals with A₁, we define x as the fraction of individuals with A₁ in the whole population (x=n/N). A good variable to describe the whole system under random variation is probability density p(x,t), which means the probability of a population with A₁ fraction of x at time t. p(x,t) satisfies the forward Kolmogorov equation

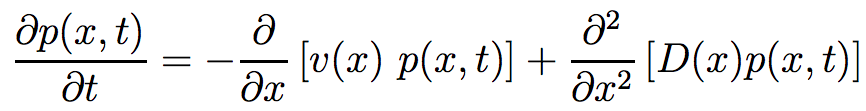
where v(x) is drift term, expressing the velocity with which transitions change:

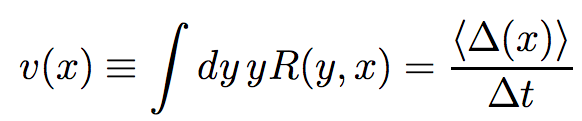
and D(x) is diffusion coefficient, characterizing the range of random variation of the probability function:

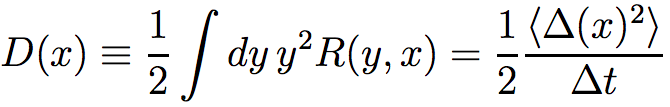
where R(y,x) is the rate of transition from state y to x. If the transition rate of A₂ A₁ (A₁ A₂) is μ₁ (μ₂), then

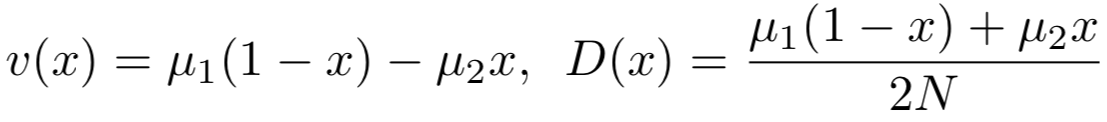
For genetic drift, if assuming no mutations (μ₁=μ₂=0), by employing binomial selection model^{see below}, we can get for diploid,

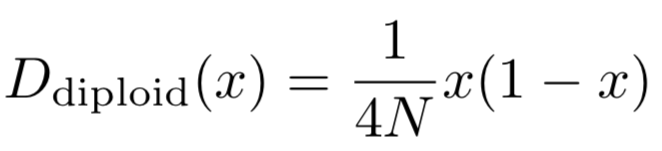
Therefore, combining these two contributions, we can have the final drift and diffusion terms:

Steady solution

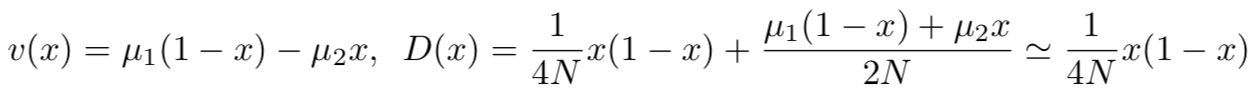
In terms of the forward Kolmogorov equation, it is interesting and technically easier to find the steady state solution to which the population settles after a long time, which is denoted as p*(x). Thus,

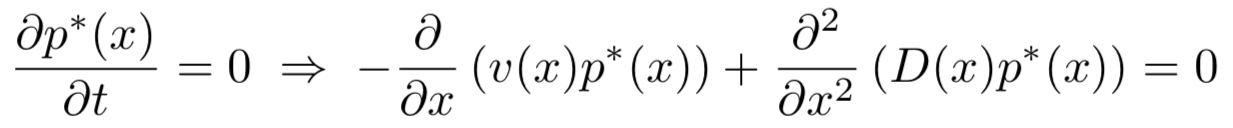
With v(x) and D(x) we find above, a steady probability density function under assumption μ₁=μ₂=μ as a function of x can be obtained:

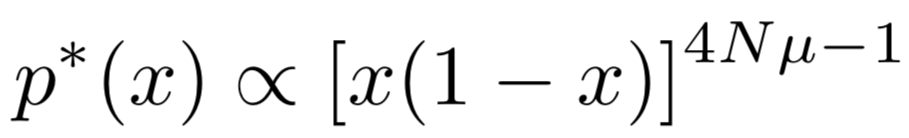
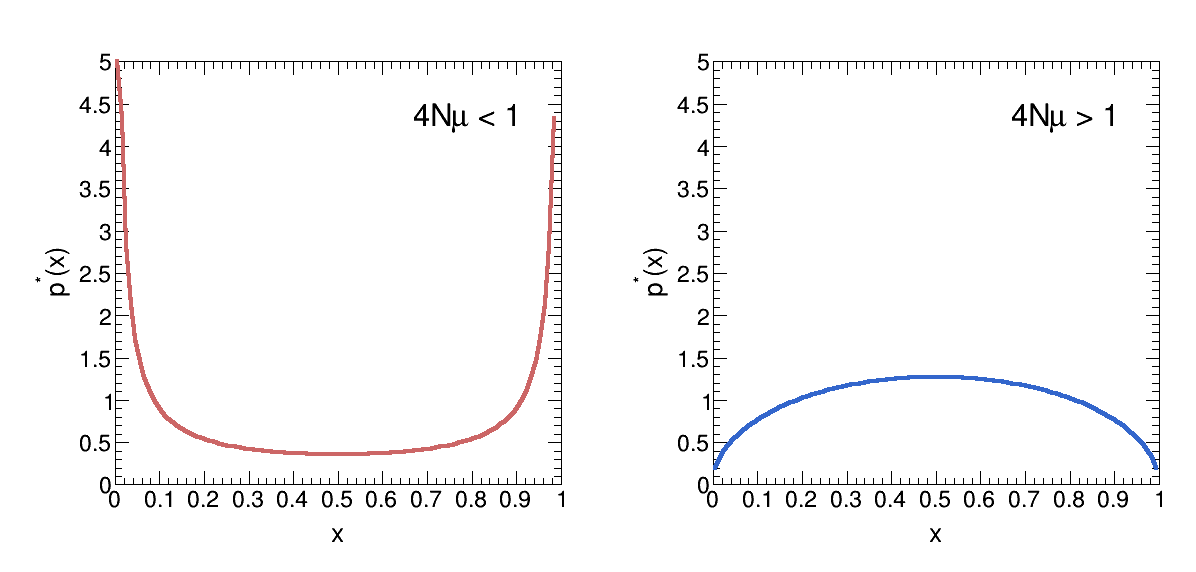
The result we just obtain is very interesting. It indicates that the behavior of the system is dramatically different with 4Nμ<1 and 4Nμ>1. We plot p*(x) for these two situations, which is shown in the plot below.

Therefore, the mutation scale is μ, and the genetic drift scale is 1/4N. When 4Nμ<1, the genetic drift is dominant, and therefore the system will reach fixation (loss) of an allele. When 4Nμ<1, the mutation is dominant, and therefore the system will reach an equilibrium at x=0.5.